积分的换元牵涉到换限,总是会迷茫。
做个总结:换元后要保持原来的积分函数不变。
对于积分元变换后,和原积分函数的值要保持不变。需要找出新的积分函数。例如极坐标变换时:
D∬f(x,y)dxdy=D′∬f(rcosθ,rsinθ)rdθdr
对应的多出了个 r 就是要保证两个积分函数在不同积分元情况下等值。
换限:即保证积分区域也要一致。
换限通过画一个坐标系比较直观:例如在概率论中多维随机变量的分布:FY/X(z)=P{Y/X≤z}
=∬y/x≤z,x<0f(x,y)dydx+∬y/x≤z,x>0f(x,y)dydx
=∫−∞0[∫zx∞f(x,y)dy]dx+∫0∞[∫−∞zxf(x,y)dy]dx
令y=xu,则:dy=xdu,代入得: f(x,y)dy=f(x,xu)xdu (1)。此部分更换后不变。
再看积分限:因dy变成du,直观来说“变换的幅度有区别了”,在下图中来看:
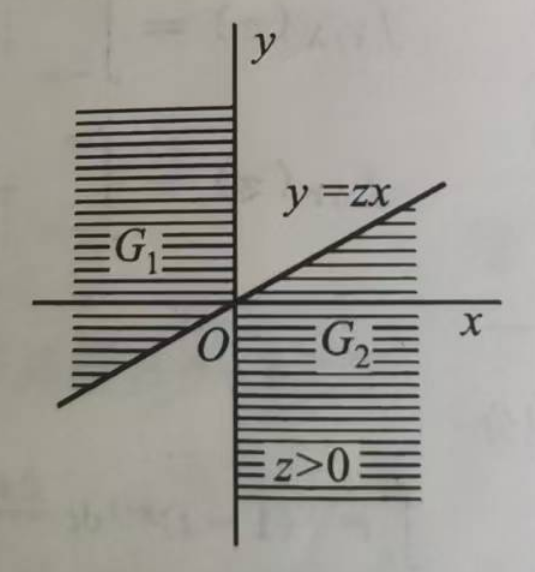
原y的积分限是图中阴影位置,y在zx这条线上方和下方阴影区域,更换积分元后,u 的变化范围如果不变,把 zx 代入式(1):
f(x,zx)dy=f(x,xzx)xdu
明显看到在最大值/最小值时是明显不相等的。所以就不能是原来的zx 作为上下限。原积分限的无穷通过加减乘除一个固定数,依然是无穷,所以无变化。原dy 积到的最大/最小值zx,换成du 后,就是u 变成什么,使得y 还是积到最大/最小值zx ,
明显是:zx=zu,保证了积分区域不变
所以则u变成z就保证了不变,第一个函数中原y上限是正无穷,变化为u后,因x<0, 所以u也必须小于0,才能保证是正无穷。第二个函数中x>0,不受影响,所以最终换元后的函数:
=∫−∞0[∫z−∞f(x,xu)xdu]dx+∫0∞[∫−∞zf(x,xu)xdu]dx
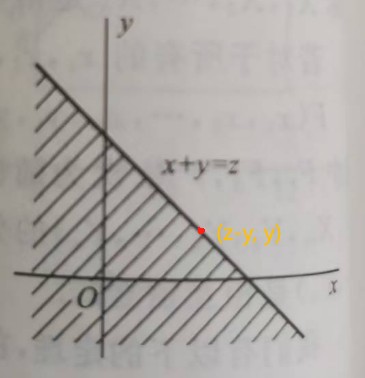
再看FX+Y(z)=P{X+Y≤z}的分布函数:∫−∞∞[∫−∞z−yf(x,y)dx]dy
令x=u−y,积分函数x,u的变化幅度是相同的dx=du,所以:f(x,y)dx=f(u−y,y)du
再看积分限:当y固定后,原x的积分范围是由−∞到z−y,现在积分元为u,无穷减去一个确定数依然是无穷,不变;上限z−y,要保证x换成u后,原x的上限不变,z−y=u−y,则u的上限变成z保证了和原x 的积分范围相同。所以:
∫−∞∞[∫−∞zf(u−y,y)du]dy